Amazing Mazes!

Introduction: What’s an algorithm?

An algorithm is a set of instructions that we follow to solve a problem. A simple example of an algorithm is a recipe – a set of instructions that we follow to prepare a (hopefully) delicious meal.

Algorithms are the most important idea in Decision Mathematics, and they are also used to program computers.

When we are using a computer to solve an algorithm, it’s often helpful to write down the algorithm either as a flowchart, or as pseudocode.

For example, here is a flowchart for a very simple algorithm that converts temperature from degrees Fahrenheit to degrees Celsius.

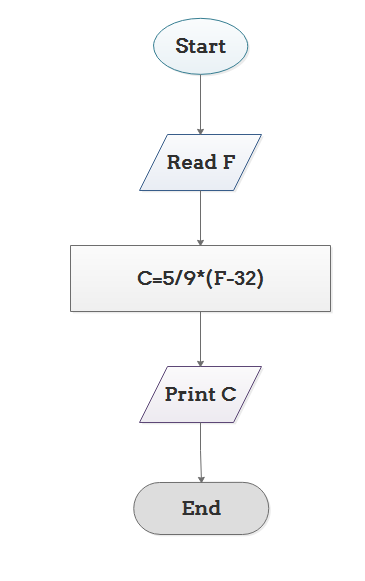
In pseudo-code, we could say:

Read the value of F

Calculate C = 5/9 * (F – 32)

Print the value of C.

Building a Maze

Let’s now think about an algorithm to build a maze. We want to build a random maze, so that it is different every time we create it.

The algorithm is called a recursive backtracking algorithm, and it works with a large grid of cells. These cells could be square, and we will show an example with hexagons in this blog.

Each cell is initially separated by walls from each other. The pseudocode below describes what we need to do to generate the maze.

(The stack referred to in the pseudocode is just a way of storing information in a computer. Items can be added to the top of the stack – you can visualise it as a pile of books, for example. When we wish to remove an item, we just remove the top item from the stack – like removing the top book from the pile).

Choose any cell as the initial cell, mark it as visited, and add it to the stack

While the stack is not empty:

1. Take a cell off the stack, and mark it as the current cell

2. If the current cell has any neighbours which have not been visited:

a. Add the current cell to the stack

b. Choose one of the unvisited neighbours

c. Remove the wall between the current cell and the chosen cell

d. Mark the chosen cell as visited and add it to the stack

This algorithm is more tricky to understand than the Fahrenheit-Celsius algorithm, so let’s explore how it works on a simple grid of square cells, initially all separated by walls. Each cell is labelled with a letter, so that we can refer to it.

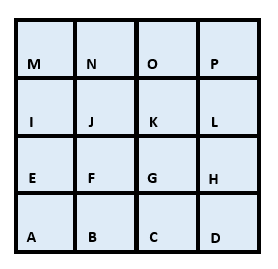
Choose any cell as the initial cell, mark it as visited, and add it to the stack:

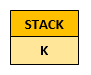
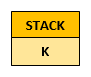
While the stack is not empty:

Take a cell off the stack, and mark it as the current cell

So: Take cell K off the stack

Mark it as visited (the star)

If the current cell has any neighbours which have not been visited:

Add the current cell to the stack

Choose one of the unvisited neighbours

(Cell G chosen)

Remove the wall between the current cell and the chosen cell

Mark the chosen cell as visited and add it to the stack

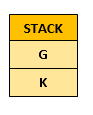
While the stack is not empty:

Take a cell off the stack, and mark it as the current cell

So: Take cell G off the stack

Mark it as visited

If the current cell has any neighbours which have not been visited:

Add the current cell to the stack

Choose one of the unvisited neighbours

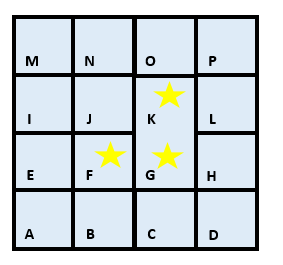
(Cell F chosen)

Remove the wall between the current cell and the chosen cell

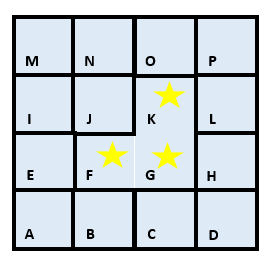
And so on …… (computers are much faster at this than humans!)

You can see that we are building up a ‘corridor’ in the maze, connecting cells F, G and K.

The other part of the algorithm kicks into action if there are no neighbours which have not been visited.

For example, let’s say that the red cells have already been visited in the grid below:

Our current cell is F, and the stack is

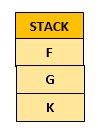
Take a cell off the stack, and mark it as the current cell

So, we take F off the stack.

The stack is now

F has no neighbours which have not been visited.

Therefore we move to point 1 in the algorithm and

Take a cell off the stack, and mark it as the current cell

So, we take G off the stack.

The stack is now

G has no neighbours which have not been visited.

Therefore we move again to point 1 in the algorithm and

Take a cell off the stack, and mark it as the current cell

So, we take K off the stack.

The stack is now

K has a neighbour which hasn’t been visited, L, and so we can move to it.

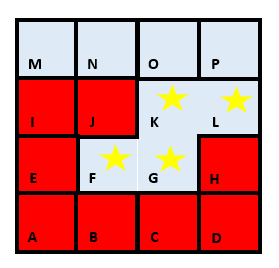
So we’ve first backtracked from F through G to K, and then started to build a new ‘corridor’ in the maze from K to L.

The recursive backtracking algorithm has only six lines of pseudocode, and yet it can randomly generate a maze for us!

The algorithm also works with any shape. Square grids are the simplest, but it will work for other shapes as well. Here are examples of random hexagonal mazes, generated using the same six steps of pseudocode.

This is a 10x10 random hexagonal maze:

And this is a much bigger 50x30 maze:

Solving a Maze

There is a very simple method for finding a path through a maze. It’s called the left hand maze solving algorithm, but works perfectly well with your right hand as well.

Here is the pseudocode:

Touch the wall with your left hand

Keep your left hand touching the wall and walk, always ensuring that your left hand is

touching the wall.

Simple!

Here an example of the algorithm used to find a path through a 10x10 maze, starting at the green dot and finishing at the red dot:

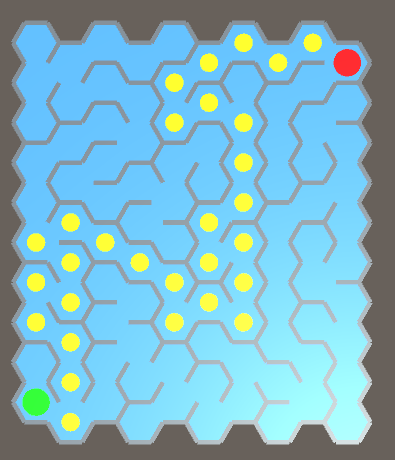
And here is an example of solving a 50x30 maze:

The left hand maze solving algorithm isn’t fast, and may take you on a very long path, but it will eventually get you out of the maze…….you’ll never get lost in a maze again!

If you are interested check out our maze generation and maze solving app!