Foxes and Rabbits!
- Andrew Daniel

- Jun 5, 2020
- 7 min read
Let’s say we have a simple world, or ecosystem, in which only two animals live: foxes and rabbits.

The foxes eat the rabbits, so the foxes can be called predators. The rabbits, if they are unlucky, get eaten by the foxes, so the rabbits can be called prey.
(The rabbits eat carrots, grass, flowers and other vegetation, and we will assume that there is always a sufficient supply of this for the rabbits to eat).
Both foxes and rabbits can be born, so that their population increases. However, both foxes and rabbits can also die, causing their population to decrease. A fox can die if it can’t get enough rabbits to eat, and a rabbit can die if it is eaten by a fox.
The populations of the foxes and rabbits will be closely linked. For example, if the population of rabbits declines, then we would expect the population of foxes to decline soon afterwards, because the foxes will have less to eat.
Similarly, if the population of foxes declines, we would expect the population of rabbits to increase, because there are less foxes to eat them.
This linked relationship between populations of predators and prey occurs throughout the natural world. We’ve discussed foxes and rabbit, but we could equally think about cheetahs and baboon, swallows and insects, sharks and fish, and so on.
Vito Volterra and Alfred Lotka
Many mathematicians have worked on the problem of predator and prey populations, because it is so important in the world.Alfred Lotka first considered this problem by looking at the theory of particular types of chemical reactions.His work is a good example of maths being transferred from one area of study to another.Vito Volterra was particularly interested in marine biology, and he studied populations of predators, including sharks and stingrays, and the fish that they preyed upon, in the Adriatic Sea.
Here is some data that Volterra collected from the Fiume port on the Adriatic.

The percentages of predators changes greatly, and Volterra noticed that it is highest towards the end and soon after World War I. Volterra suggested that fishing was reduced greatly during the war, and as a consequence fish stocks increased. In turn, the population of predators increased, because more food was available.
Volterra developed a series of mathematical models to explain the relationships between predators and prey. Lotka, working in America, developed similar models at the same time. We will consider the simplest of their models here.
A Predator-Prey Mathematical Model
In maths a model is a way in which we try to represent something in the real world, using mathematics. To do this, we always have to make big simplifications. These are called assumptions.
Volterra and Lotka made these assumptions:
Predators only eat the prey as food – there are no other sources of food for them
The prey has an unlimited food supply and the only thing that eats it is the predator.
Let’s follow the reasoning of Lotka and Volterra as they developed their mathematical model.
Prey
First let’s have a very simple world with only prey, and no predators.
In this case, as the prey have unlimited food, the prey population will grow exponentially. This means that the increase in the prey population at any time will be proportional to the size of the population at that time.
Therefore

where x is the prey population, dx/dt is the rate of change of the prey population, and a is a constant which represents the birth rate of the prey.
This is a first order differential equation, which we can solve by separating the variables.

and so

where c is an integration constant.Therefore

where X is the initial population of the prey.
This equation with X = 10 and a = 1 gives us a graph like this:

This is the familiar exponential growth graph.
Now we will introduce predators into the world. These will cause the prey population to grow less quickly, as the predators eat the prey.
Lotka and Volterra made two assumptions about predators in their model:
The rate at which predators encounter prey is proportional to both the size of the predator population, and the size of the prey population
A fixed proportion of encounters leads to the death of the prey.
Let’s say the predator population is size y at time t. These two assumptions mean that a negative component of the prey growth rate is proportional to the product xy of the population sizes. Our equation needs an extra term like this:

where b is a constant that represents the death rate of prey.
One way to explore this equation is to set y to be a constant, so the population of the predator is fixed.This isn’t at all realistic, but at least gives us a way to solve the equation.If y is constant, the equation can be written as

which eventually rearranges to

This equation with X = 10, y = 1, a = 1, b = 0.5, and t = 1 gives us a graph like this:

The new red curve is plotted against the earlier blue curve (which had no predators), to show the effect of the one constant predator in slowing the prey population growth.
Predators
We’ll now think about the predator population. First, let’s think about a world with predators and no prey, so there is no food for the predators.
In this case the predators will die out at a rate proportional to the population size y, so that

where c is the death rate of the predators.
We can solve this equation using the same method as above, to give
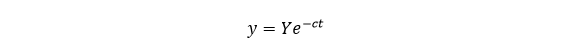
where Y is the initial predator population.
This equation with Y = 10 and c = 1 gives us a graph like this:

This type of graph is called an exponential decay graph.
Now we will introduce prey into our predator world. As above, we will assume that the rate at which predators encounter prey is proportional to both the size of the predator population, and the size of the prey population. As predators eat prey, this will support growth of the predator population, and so a positive term can be added to our equation above:

where d is a constant representing the growth rate of predators.
The Lotka-Volterra Predator-Prey Model
We’ve discussed prey and predators separately so far. Now let’s combine them to produce a full model for predator and prey populations:
This is the equation for the prey:

and this is for the predators

The two differential equations are coupled, because one needs the other to work out the answer, and vice versa.
The equations contain four constants:
a representing the birth rate of prey
b representing the death rate of prey
c representing the death rate of predators
d representing the birth rate of predators.
Although we could solve the single differential equations, above, without too much difficulty, it’s very challenging to solve two coupled differential equations using algebra.
However, we can find approximate solutions to the equations using numerical methods.
We will approximate the rates of change of prey and predator populations over a time step, Δt. This time step could be 1 hour, or 1 minute, for example. Then:

where Δx and Δy are the changes in the prey and predator populations over the time step.
The Lotka-Volterra equations become

So given the current populations of prey and predators, x and y, the four constants and the time step Δt, we can work out the change in the prey population, Δx, and the predator population, Δy, over the time step.
We can then repeat this calculation again and again, over a large number of time steps, to predict the predator and prey populations in the future.
This method, using a time step, is called a finite difference method. Because we are calculating forwards in time, it is a forward-difference method.
Predicting Predator-Prey Populations
Excel is a great way to calculate with the finite different method. But first let’s calculate over a couple of time steps so that we understand the method.
We will take values for the constants of a = 1.1, b = 0.4, c = 0.4, and d = 0.1. The time step will be 0.1.
The initial values of x and y will be 10.
After the first time step:

so Δx = -29 x 0.1 = -2.9 and Δy = 6 x 0.1 = 0.6.
The new value of x is 10 – 2.9 = 7.1, and the new value of y is 10 + 0.6 = 10.6.
(Don’t worry about decimal values, because x and y could represent population sizes in 1000s, for example. It doesn’t mean we have 0.6 of a fox!)
After the second time step:

which gives a new value of x = 4.8706, and a new value of y = 10.9286.
But this is all much easier with Excel!
Here is the table of the first few population values, calculated by Excel:

This is a graph of prey (x) and predator (y) populations with time.

You can see the relationships between the two curves, and note in particular that the peaks in the predator population occur slightly after the peaks in the prey population. Predators increase their numbers as the availability of prey increases, but then as a prey population drops the predators start to lose their food source.
Simulation of Predator-Prey Populations
A simulation on a computer is where we try to program a computer to imitate something that happens in the natural world.
So we will try to simulate a predator-prey system in a 3D computer-generated world with rabbits and foxes.

We start by selecting the initial numbers of rabbits and foxes for the simulation.
Then select ‘programmed’ (in which the movement of animals is explicitly programmed) or ‘neural networked’ (in which the movement of animals is controlled by an artificial intelligence algorithm).
In the simulation we will have foxes which can eat rabbits (the loud crunch sound) if they manage to catch them.

Rabbits will eat flowers (the quiet crunch sound) and the flowers repollenate (i.e. produce lots more flowers) when flower population drops below minimum value. This ensures a constant supply of food for the rabbits.

Both rabbits and foxes can mate to produce babies (you can see this with the love heart symbols flying into the air, from time to time).
Both animals also get thirsty, and so they have to seek out water to drink.
Both animals can occasionally drown (falling into water) or die by old age.
The simulation shows how populations of foxes and rabbits change over time (when a population approaches 1000 most desktop computers may start to run slowly). By changing the initial populations, you should be able to create worlds in which either rabbits dominate, or the foxes dominate.




Comments