Musical Maths!
- Andrew Daniel

- Jun 10, 2020
- 6 min read
Updated: Jun 14, 2020
Did you know that the great composer Johan Sebastian Bach (1685 – 1750) was also very good at maths? In this blog you’ll discover how Bach used maths to completely reinvent music. Bach’s maths created the music that we listen to today.
But first, we’ll need to understand a few important aspects of the history of numbers ……..
A Very Brief History of Numbers
Once upon a time, many years ago, the only type of numbers known were counting numbers: positive, whole numbers. This is an infinite set of numbers, starting with 1:
{1, 2, 3, 4, 5, 6, ……}.
There is evidence of counting using whole numbers from about 20,000 years ago.The Ishango Bone, shown below, is an animal bone dating from this time.The bone has a series of notches carved into it, which shows that Stone Age man was using a tally for counting.

So counting numbers have been used for at least 20,000 years. Around 1600BC, the ancient Egyptians started to use fractions. Many pupils at school have learned to loath fractions, but they are a much more fundamental kind of number than decimals. Decimals were invented more recently, and only really became important when calculators were used in maths.
The Rhind Papyrus provided archaeological evidence for the way that Egyptians used fractions:

Fractions are also called rational numbers, and they are created by taking one whole number (called the numerator) and dividing it by another (called the denominator). When the Egyptians used fractions, they only used numerators of 1, which made some of their fractions calculations tricky!
When we look at the link between maths and music, it’s important to understand that fractions are numbers that allow us to fill in the gaps between whole numbers, on a number line.
For example, this is a number line with just counting numbers:
Fractions allow us to fill in the gaps between the counting numbers, like this:

For a long time mathematicians thought that fractions could completely fill the gaps between counting numbers on the number line. Mathematicians thought that with counting numbers and fractions, and negative numbers also, they had found all of the types of numbers that existed.
Unfortunately at this point in history mathematicians were completely and utterly wrong!
For example, it’s reasonably straightforward to show that the square root of 2 (approximately 1.41) is impossible to write as a fraction. It’s worth looking up this proof: it is a great example of proof by contradiction, and it proves that there are numbers on the number line that can’t be written as fractions.
The number π, the circumference of a circle divided by the diameter (approximately 3.14), is also impossible to write as a fraction (although this is much harder to prove).
These numbers that can’t be written as fractions are called irrational numbers, and it turns out that there are more of them on the number line than there are fractions!
Before we link this to music, let’s summarise what we have found so far:
On a number line we can show fractions, which are one whole number divided by another whole number
On a number line we can also show irrational numbers, which are impossible to write as a fraction.
Fractions and Music
Let’s say that we have a string on a musical instrument tuned to the note.
If we halve the length of this string, the note increases in pitch by an octave, to the higher C.
The important thing to understand in the maths that we’ve done is that we have multiplied the length of the string by a fraction of one half.
If we take two thirds of the length of the string, so multiply the length by the fraction 2/3, this increases the pitch of the note by a fifth, to the musical note G.
The maths description for this is that the frequency or pitch of the note is inversely proportional to the length of the string.
If we halve the length of the string, the frequency is twice as high. This is called an octave.
If we take 2/3 of the length of the string, the frequency is 3/2 times as high. This is called a perfect fifth.
If we were to take 4/5 of the length of the string, the frequency would be 5/4 times as high. This is called a perfect third: if the bottom note is C, this would form the musical note E.
By changing the length of the string we are starting to produce a musical scale. This is what we have worked out so far:

(The frequencies shown aren’t actual frequencies, but are just relative to the low C frequency set to 1.)
These are the first notes on the C-Major scale. Let’s fill in the other notes.
F is a perfect fifth downwards from the high C, so we can calculate F as 2 ÷ 3/2 = 4/3.

The ratio from F to G is 3/2 ÷ 4/3 = 9/8. This is the same as the ratio from low C to D, so D must be 1 x 9/8 = 9/8.
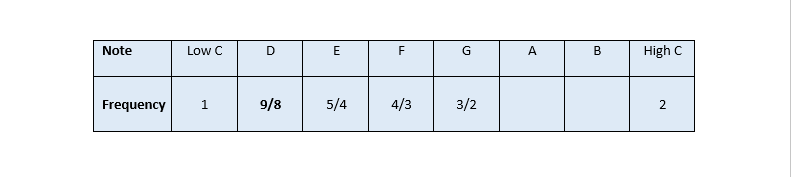
The ratio from G to B is the same as the ratio from low C to E
So B = 3/2 x 5/4 = 15/8.

And finally ……. the ratio from D to B is the same as the ratio from low C to A
So A = 15/8 ÷ 9/8 = 5/3.

This musical scale is called the Just Scale, and this was the scale used to play music until the time of Johan Sebastian Bach. The important thing to understand is that the frequencies of all of the notes are exact fractions (i.e. rational numbers), formed by dividing a string on a musical instrument into an exact fraction.
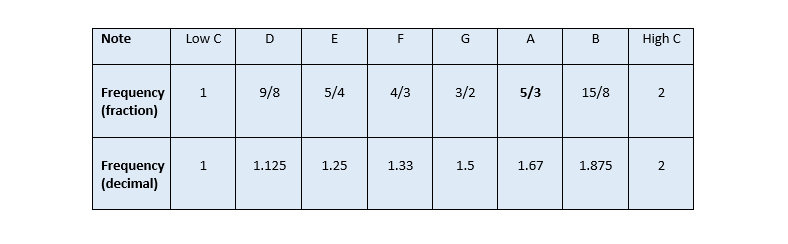
Here is the Just Scale with frequencies both as fractions, and as decimals:
Problems with the Just Scale
Unfortunately there are some serious problems with the Just Scale. The ratio of frequencies between notes changes!
For example, the ratio from C to D = 1.125 ÷ 1 = 1.125
The ratio is different from D to E: 1.25 ÷ 1.125 = 1.111
And the ratio is different again from F to G: 1.5 ÷ 1.333 = 1.0664.
The differences in these ratios mean that a musical instrument tuned perfectly for one key would then be slightly out-of-tune in any other key.
This isn’t a problem for stringed instruments, because the players can adjust the pitch of notes that they make by moving the position of their fingers slightly and changing the length of the string.
However, pre-tuned instruments like keyboards don’t have this flexibility, and so this causes a big problem when playing music on keyboards.
Johan Sebastian Bach’s Solution: The Well-Tempered Scale
Johan Sebastian Bach was the first to realise that the Just Scale would not work for music, at a time when the use of keyboards was becoming more widespread in music. Therefore, he used some great maths to invent a new scale, the Well-Tempered Scale.

There are twelve semi-tones between low C and high C, over an octave.
Bach proposed an equal ratio of frequency between any two semi-tones, so that the pitch changes constantly between semi-tones.
The frequency ratio between low C and high C is 2, and therefore the frequency ratio across a semi-tone is given by

(The twelfth root of 2 means a number that is multiplied by itself twelve times to give 2).
We can build up the well-tempered scale using this number.
C# is a semi-tone above C, and so is approximately given by 1 x 1.059 = 1.059.
D is a semi-tone above C#, and so is 1.059 x 1.059 = 1.122

And so onwards ………
Here is a comparison of the frequencies, in decimals, between the Just Scale and the Well-Tempered Scale.

For example, we can see that the third (E) of the well-tempered scale is slightly sharp, while the fifth (G) is flat.
Irrational Numbers and the Well-Tempered Scale
The notes in the well-tempered scale are all calculated using 12√2. Like the square root of 2, this is an irrational number: it cannot be written as a fraction.
For a musician, this means that it is impossible to create a fraction of a string by the amount 12√2. Therefore, the frequencies in the well-tempered scale are always approximations, because they are impossible to write as exact fractions.
So we’ve proved mathematically that the well-tempered scale can never be perfectly in tune!



Comments